How to Draw on the Xyz Plane

Mathematical puzzle of avoiding crossings

"Water, gas and electricity" redirects here. For the utilities, see Public utility. For the novel Sewer, Gas & Electric, see Matt Ruff.

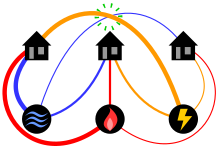
Diagram of the three utilities problem showing lines in a plane. Can each house be connected to each utility, with no connection lines crossing?

2 views of the utility graph, also known as the Thomsen graph or ${\displaystyle K_{3,3}}$

The classical mathematical puzzle known as the 3 utilities problem or sometimes water, gas and electricity asks for non-crossing connections to be drawn betwixt iii houses and three utility companies in the plane. When posing it in the early on 20th century, Henry Dudeney wrote that it was already an quondam problem. It is an impossible puzzle: it is not possible to connect all nine lines without crossing. Versions of the problem on nonplanar surfaces such as a torus or Möbius strip, or that let connections to pass through other houses or utilities, can be solved.

This puzzle tin can be formalized as a trouble in topological graph theory by request whether the consummate bipartite graph ${\displaystyle K_{3,3}}$ , with vertices representing the houses and utilities and edges representing their connections, has a graph embedding in the plane. The impossibility of the puzzle corresponds to the fact that ${\displaystyle K_{iii,3}}$ is non a planar graph. Multiple proofs of this impossibility are known, and form part of the proof of Kuratowski's theorem characterizing planar graphs past 2 forbidden subgraphs, one of which is ${\displaystyle K_{3,3}}$ . The question of minimizing the number of crossings in drawings of consummate bipartite graphs is known every bit Turán'due south brick factory problem, and for ${\displaystyle K_{3,3}}$ the minimum number of crossings is one.

${\displaystyle K_{3,3}}$ is a graph with half dozen vertices and nine edges, often referred to as the utility graph in reference to the trouble.^[1] It has also been called the Thomsen graph after 19th-century pharmacist Julius Thomsen. It is a well-covered graph, the smallest triangle-free cubic graph, and the smallest non-planar minimally rigid graph.

History [edit]

A review of the history of the three utilities trouble is given by Kullman (1979). He states that most published references to the problem narrate information technology every bit "very ancient".^[2] In the earliest publication found by Kullman, Henry Dudeney (1917) names it "water, gas, and electricity". Still, Dudeney states that the trouble is "every bit old as the hills...much older than electric lighting, or even gas".^[3] Dudeney as well published the same puzzle previously, in The Strand Magazine in 1913.^[4] A competing merits of priority goes to Sam Loyd, who was quoted by his son in a posthumous biography as having published the trouble in 1900.^[five]

Another early on version of the problem involves connecting three houses to three wells.^[6] Information technology is stated similarly to a dissimilar (and solvable) puzzle that also involves 3 houses and three fountains, with all three fountains and one house touching a rectangular wall; the puzzle once more involves making non-crossing connections, but only between three designated pairs of houses and wells or fountains, as in modern numberlink puzzles.^[7] Loyd's puzzle "The Quarrelsome Neighbors" similarly involves connecting 3 houses to three gates by three non-crossing paths (rather than 9 as in the utilities problem); one house and the three gates are on the wall of a rectangular yard, which contains the other two houses inside it.^[8]

Besides as in the iii utilities problem, the graph ${\displaystyle K_{3,3}}$ appears in late 19th-century and early 20th-century publications both in early studies of structural rigidity^{[9] [10]} and in chemic graph theory, where Julius Thomsen proposed it in 1886 for the then-uncertain construction of benzene.^[xi] In laurels of Thomsen's piece of work, ${\displaystyle K_{3,3}}$ is sometimes called the Thomsen graph.^[12]

Argument [edit]

The three utilities problem can exist stated as follows:

Suppose iii houses each need to be connected to the water, gas, and electricity companies, with a separate line from each house to each company. Is in that location a way to make all nine connections without any of the lines crossing each other?

The trouble is an abstract mathematical puzzle which imposes constraints that would not exist in a practical technology situation. Its mathematical formalization is part of the field of topological graph theory which studies the embedding of graphs on surfaces. An important part of the puzzle, just one that is often not stated explicitly in informal wordings of the puzzle, is that the houses, companies, and lines must all be placed on a two-dimensional surface with the topology of a aeroplane, and that the lines are not allowed to pass through other buildings; sometimes this is enforced past showing a drawing of the houses and companies, and asking for the connections to be drawn as lines on the aforementioned drawing.^{[13] [14]}

In more formal graph-theoretic terms, the trouble asks whether the complete bipartite graph ${\displaystyle K_{iii,3}}$ is a planar graph. This graph has six vertices in two subsets of three: one vertex for each firm, and ane for each utility. It has nine edges, i border for each of the pairings of a house with a utility, or more abstractly ane edge for each pair of a vertex in one subset and a vertex in the other subset. Planar graphs are the graphs that tin can be drawn without crossings in the aeroplane, and if such a drawing could be found, information technology would solve the three utilities puzzle.^{[13] [14]}

Puzzle solutions [edit]

Unsolvability [edit]

Proof without words: One business firm is temporarily deleted. The lines connecting the remaining houses with the utilities separate the plane into three regions. Whichever region the deleted house is placed into, the similarly shaded utility is exterior the region. By the Jordan curve theorem, a line connecting them must intersect one of the existing lines.

As it is usually presented (on a flat two-dimensional aeroplane), the solution to the utility puzzle is "no": there is no way to brand all nine connections without any of the lines crossing each other. In other words, the graph ${\displaystyle K_{3,three}}$ is non planar. Kazimierz Kuratowski stated in 1930 that ${\displaystyle K_{iii,3}}$ is nonplanar,^[15] from which it follows that the trouble has no solution. Kullman (1979), however, states that "Interestingly enough, Kuratowski did not publish a detailed proof that [ ${\displaystyle K_{3,3}}$ ] is not-planar".^[2]

One proof of the impossibility of finding a planar embedding of ${\displaystyle K_{3,3}}$ uses a example analysis involving the Hashemite kingdom of jordan bend theorem.^[16] In this solution, ane examines different possibilities for the locations of the vertices with respect to the iv-cycles of the graph and shows that they are all inconsistent with a planar embedding.^[17]

Alternatively, it is possible to evidence that whatever bridgeless bipartite planar graph with ${\displaystyle Five}$ vertices and ${\displaystyle East}$ edges has ${\displaystyle E\leq 2V-4}$ by combining the Euler formula ${\displaystyle V-East+F=2}$ (where ${\displaystyle F}$ is the number of faces of a planar embedding) with the observation that the number of faces is at virtually half the number of edges (the vertices effectually each face must alternating betwixt houses and utilities, so each face has at least four edges, and each border belongs to exactly ii faces). In the utility graph, ${\displaystyle E=9}$ and ${\displaystyle 2V-4=8}$ so in the utility graph it is untrue that ${\displaystyle E\leq 2V-four}$ . Because it does not satisfy this inequality, the utility graph cannot be planar.^[xviii]

Irresolute the rules [edit]

Solution on a torus

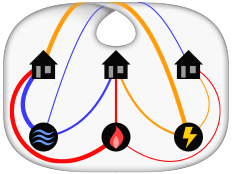
Solution on a Möbius strip

${\displaystyle K_{3,three}}$ is a toroidal graph, which means that it can be embedded without crossings on a torus, a surface of genus ane.^[19] These embeddings solve versions of the puzzle in which the houses and companies are fatigued on a coffee mug or other such surface instead of a flat plane.^[twenty] There is fifty-fifty enough boosted freedom on the torus to solve a version of the puzzle with four houses and four utilities.^{[21] [5]} Similarly, if the iii utilities puzzle is presented on a canvass of a transparent material, it may exist solved later on twisting and gluing the canvass to form a Möbius strip.^[22]

Another way of changing the rules of the puzzle that would make it solvable, suggested past Henry Dudeney, is to allow utility lines to pass through other houses or utilities than the ones they connect.^[3]

Backdrop of the utility graph [edit]

Beyond the utility puzzle, the aforementioned graph ${\displaystyle K_{iii,iii}}$ comes upwards in several other mathematical contexts, including rigidity theory, the classification of cages and well-covered graphs, the written report of graph crossing numbers, and the theory of graph minors.

Rigidity [edit]

The utility graph ${\displaystyle K_{3,three}}$ is a Laman graph, meaning that for about all placements of its vertices in the plane, there is no manner to continuously motion its vertices while preserving all border lengths, other than by a rigid motion of the whole plane, and that none of its spanning subgraphs have the same rigidity property. It is the smallest example of a nonplanar Laman graph.^[23] Despite being a minimally rigid graph, it has non-rigid embeddings with special placements for its vertices.^{[ix] [24]} For full general-position embeddings, a polynomial equation describing all possible placements with the same edge lengths has degree 16, meaning that in general in that location can be at almost 16 placements with the same lengths. It is possible to notice systems of edge lengths for which upwards to eight of the solutions to this equation describe realizable placements.^[24]

Other graph-theoretic properties [edit]

${\displaystyle K_{3,3}}$ is a triangle-costless graph, in which every vertex has exactly three neighbors (a cubic graph). Among all such graphs, it is the smallest. Therefore, it is the (3,4)-cage, the smallest graph that has three neighbors per vertex and in which the shortest cycle has length four.^[25]

Like all other complete bipartite graphs, it is a well-covered graph, meaning that every maximal contained set has the aforementioned size. In this graph, the but 2 maximal contained sets are the 2 sides of the bipartition, and are of equal sizes. ${\displaystyle K_{3,3}}$ is 1 of merely seven 3-regular 3-connected well-covered graphs.^[26]

Generalizations [edit]

Cartoon of ${\displaystyle K_{three,three}}$ with i crossing

Ii important characterizations of planar graphs, Kuratowski'south theorem that the planar graphs are exactly the graphs that contain neither ${\displaystyle K_{3,3}}$ nor the consummate graph ${\displaystyle K_{5}}$ as a subdivision, and Wagner's theorem that the planar graphs are exactly the graphs that incorporate neither ${\displaystyle K_{3,iii}}$ nor ${\displaystyle K_{5}}$ as a minor, make use of and generalize the non-planarity of ${\displaystyle K_{3,3}}$ .^[27]

Pál Turán's "brick factory problem" asks more generally for a formula for the minimum number of crossings in a drawing of the complete bipartite graph ${\displaystyle K_{a,b}}$ in terms of the numbers of vertices ${\displaystyle a}$ and ${\displaystyle b}$ on the two sides of the bipartition. The utility graph ${\displaystyle K_{3,iii}}$ may be drawn with merely one crossing, simply not with cypher crossings, then its crossing number is 1.^{[five] [28]}

References [edit]

1. ^ Gries, David; Schneider, Fred B. (1993), "Chapter nineteen: A theory of graphs", A Logical Approach to Discrete Math, New York: Springer, p. 423–460, doi:ten.1007/978-i-4757-3837-7, ISBN978-one-4419-2835-1, S2CID 206657798 . See p. 437: " ${\displaystyle K_{three,3}}$ is known as the utility graph".
2. ^ ^{a b} Kullman, David (1979), "The utilities problem", Mathematics Mag, 52 (5): 299–302, doi:10.1080/0025570X.1979.11976807, JSTOR 2689782
3. ^ ^{a b} Dudeney, Henry (1917), "Problem 251 – H2o, Gas, and Electricity", Amusements in mathematics, vol. 100, Thomas Nelson, p. 73, Bibcode:1917Natur.100..302., doi:10.1038/100302a0, S2CID 10245524 . The solution given on pp. 200–201 involves passing a line through one of the other houses.
4. ^ Dudeney, Henry (1913), "Perplexities, with some easy puzzles for beginners", The Strand Magazine, vol. 46, p. 110
5. ^ ^{a b c} Beineke, Lowell; Wilson, Robin (2010), "The early on history of the brick mill trouble", The Mathematical Intelligencer, 32 (2): 41–48, doi:ten.1007/s00283-009-9120-iv, MR 2657999, S2CID 122588849
6. ^ "Puzzle", Successful Farming, vol. 13, p. fifty, 1914 ; "A well and firm puzzle", The Youth's Companion, vol. xc, no. 2, p. 392, 1916 .
7. ^ "32. The fountain puzzle", The Sorcerer'southward Own Book, Or, The Whole Art of Conjuring, New York: Dick & Fitzgerald, 1857, p. 276
8. ^ Loyd, Sam (1959), "82: The Quarrelsome Neighbors", in Gardner, Martin (ed.), Mathematical Puzzles of Sam Loyd, Dover Books, p. 79, ISBN9780486204987
9. ^ ^{a b} Dixon, A. C. (1899), "On certain deformable frameworks", Messenger of Mathematics, 29: 1–21, JFM 30.0622.02
10. ^ Henneberg, L. (1908), "Die graphische Statik der starren Körper", Encyklopädie der Mathematischen Wissenschaften, vol. 4, pp. 345–434 . See in item p. 403.
11. ^ Thomsen, Julius (July 1886), "Die Constitution des Benzols" (PDF), Berichte der Deutschen Chemischen Gesellschaft, 19 (2): 2944–2950, doi:10.1002/cber.188601902285
12. ^ Bollobás, Béla (1998), Modern Graph Theory, Graduate Texts in Mathematics, vol. 184, Springer-Verlag, New York, p. 23, doi:10.1007/978-1-4612-0619-iv, ISBN0-387-98488-7, MR 1633290
13. ^ ^{a b} Harary, Frank (1960), "Some historical and intuitive aspects of graph theory", SIAM Review, 2 (2): 123–131, Bibcode:1960SIAMR...two..123H, doi:10.1137/1002023, MR 0111698
14. ^ ^{a b} Bóna, Miklós (2011), A Walk Through Combinatorics: An Introduction to Enumeration and Graph Theory, World Scientific, pp. 275–277, ISBN9789814335232 . Bóna introduces the puzzle (in the course of three houses to exist connected to three wells) on p. 275, and writes on p. 277 that it "is equivalent to the problem of drawing ${\displaystyle K_{three,3}}$ on a plane surface without crossings".
15. ^ Kuratowski, Kazimierz (1930), "Sur le problème des courbes gauches en topologie" (PDF), Fundamenta Mathematicae (in French), 15: 271–283, doi:10.4064/fm-15-1-271-283
16. ^ Ayres, W. L. (1938), "Some elementary aspects of topology", The American Mathematical Monthly, 45 (2): 88–92, doi:ten.1080/00029890.1938.11990773, JSTOR 2304276, MR 1524194
17. ^ Trudeau, Richard J. (1993), Introduction to Graph Theory, Dover Books on Mathematics, New York: Dover Publications, pp. 68–seventy, ISBN978-0-486-67870-2
18. ^ Kappraff, Jay (2001), Connections: The Geometric Span Between Art and Science, K & E Serial on Knots and Everything, vol. 25, Globe Scientific, p. 128, ISBN9789810245863
19. ^ Harary, F. (1964), "Recent results in topological graph theory", Acta Mathematica, 15 (3–4): 405–411, doi:10.1007/BF01897149, hdl:2027.42/41775, MR 0166775, S2CID 123170864 ; see p. 409.
20. ^ Parker, Matt (2015), Things to Make and Practise in the Time: A Mathematician'southward Journey Through Narcissistic Numbers, Optimal Dating Algorithms, at Least Ii Kinds of Infinity, and More, New York: Farrar, Straus and Giroux, pp. 180–181, 191–192, ISBN978-0-374-53563-six, MR 3753642
21. ^ O'Beirne, T. H. (December 21, 1961), "Christmas puzzles and paradoxes, 51: For boys, men and heroes", New Scientist, vol. 12, no. 266, pp. 751–753
22. ^ Larsen, Mogens Esrom (1994), "Misunderstanding my mazy mazes may make me miserable", in Guy, Richard K.; Woodrow, Robert E. (eds.), Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History held at the University of Calgary, Calgary, Alberta, August 1986, MAA Spectrum, Washington, DC: Mathematical Clan of America, pp. 289–293, ISBN0-88385-516-X, MR 1303141 . See Figure 7, p. 292.
23. ^ Streinu, Ileana (2005), "Pseudo-triangulations, rigidity and motion planning", Discrete & Computational Geometry, 34 (4): 587–635, doi:10.1007/s00454-005-1184-0, MR 2173930, S2CID 25281202 . Encounter p. 600: "Non all generically minimally rigid graphs have embeddings every bit pseudo-triangulations, because not all are planar graphs. The smallest example is ${\displaystyle K_{3,3}}$ ".
24. ^ ^{a b} Walter, D.; Husty, M. L. (2007), "On a nine-bar linkage, its possible configurations and conditions for paradoxical mobility" (PDF), in Merlet, Jean-Pierre; Dahan, Marc (eds.), 12th World Congress on Mechanism and Machine Science (IFToMM 2007), International Federation for the Promotion of Mechanism and Machine Scientific discipline
25. ^ Tutte, W. T. (1947), "A family of cubical graphs", Proceedings of the Cambridge Philosophical Society, 43 (4): 459–474, Bibcode:1947PCPS...43..459T, doi:10.1017/s0305004100023720, MR 0021678
26. ^ Campbell, South. R.; Ellingham, M. Due north.; Royle, Gordon F. (1993), "A characterisation of well-covered cubic graphs", Journal of Combinatorial Mathematics and Combinatorial Computing, xiii: 193–212, MR 1220613
27. ^ Little, Charles H. C. (1976), "A theorem on planar graphs", in Casse, Louis R. A.; Wallis, Walter D. (eds.), Combinatorial Mathematics IV: Proceedings of the Fourth Australian Conference Held at the Academy of Adelaide August 27–29, 1975, Lecture Notes in Mathematics, vol. 560, Springer, pp. 136–141, doi:ten.1007/BFb0097375, MR 0427121
28. ^ Pach, János; Sharir, Micha (2009), "5.1 Crossings—the Brick Factory Problem", Combinatorial Geometry and Its Algorithmic Applications: The Alcalá Lectures, Mathematical Surveys and Monographs, vol. 152, American Mathematical Social club, pp. 126–127

External links [edit]

• three Utilities Puzzle at Cutting-the-knot
• The Utilities Puzzle explained and "solved" at Archimedes-lab.org
• Weisstein, Eric Due west., "Utility graph", MathWorld

berrywhispiever.blogspot.com

Source: https://en.wikipedia.org/wiki/Three_utilities_problem